# {*no-status title-slide custom-title} // comment - Authors: Valentina Zantedeschi, Rémi Emonet, Marc Sebban - Date: - Lille - Magnet Team

## Soft-Margin SVM
for a sample $S$ of $m$ instances $(x_i,y_i)$ $argmin_{\theta,b}\:\: \frac{1}{2} \left\| \theta \right\|_2^2 + c \sum_i \xi_i $ $s.t. \:\:\: y_i \left( \theta^T \mu(x_i) + b \right) \geq 1- \xi_i \:,\:$ $\xi_i \geq 0$
- $\theta$, $b$ the parameters of the linear separator - $\mu$ a mapping function, so that $\mu(x_i)^T\mu(x_j) = K(x_i,x_j)$ ## Supervised Learning

In Brief

- Learning a classifier from a fully labeled set

Issues

- Label assignment is difficult and expensive: - difficult: unique and reliable labels - expensive: great amount of data, need for experts - Datasets are generally noisy
How to handle the confidence in the labels? ## Weak-Label Learning labels are incorrect, missing or not unique

Sub-problems

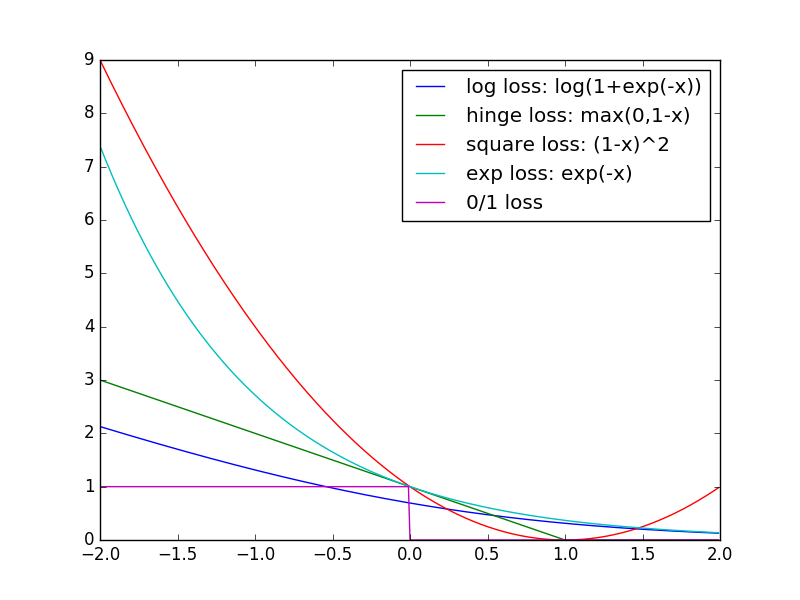
- Semi-Supervised Learning - Unsupervised Learning - Label Proportions Learning - Multi-Instance Learning - Multi-Expert Learning - Noisy-Tolerant Learning ## Empirical Surrogate $\beta$-Risk
For any margin-based loss function $ F_{\phi} $ $R_{\phi}^{\beta}(X,h) = \frac{b_{\phi}}{m} \sum_{i=1}^{m} \sum_{\sigma \in -1,1} \beta_i^{\sigma} F_{\phi}(\sigma h(x_i))$

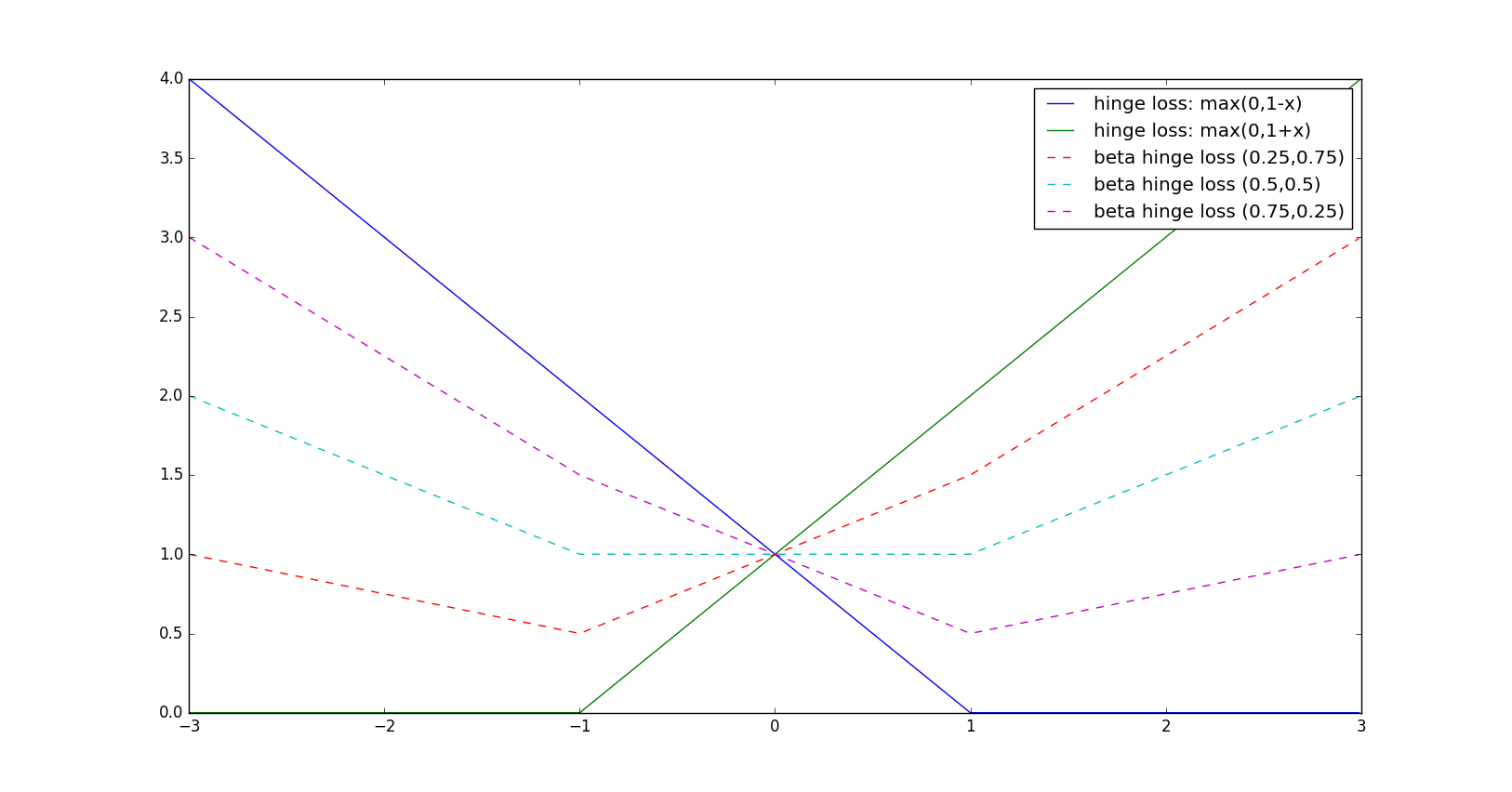
$\beta$ degree of confidence / probability of labels $\beta_i^{\text{-}1} \in [0,1]$, $\beta_i^{\text{+}1} \in [0,1]$ $ \beta_i^{\text{-}1} + \beta_i^{\text{+}1} = 1 $

Margin-based loss functions

## Soft-Margin $\beta$-SVM
primal problem $argmin_{\theta,b}\:\: \frac{1}{2} \left\| \theta \right\|_2^2 + c \sum_i \left(\beta_i^{\text{-}1}\xi_i^{\text{-}1}+\beta_i^{\text{+}1}\xi_i^{\text{+}1} \right)$ $s.t. \:\:\: \sigma (\theta^T \mu(x_i) + b) \geq 1- \xi_i^{\sigma} \:,\:$ $\xi_i^{\sigma} \geq 0$ Lagrangian dual problem $\max_{\alpha} \:\: -\frac{1}{2} \sum_{i,j} \sum_{\sigma,{\sigma}'} \alpha_i^{\sigma} \sigma \alpha_j^{{\sigma}'} {\sigma}' K(x_i,x_j) + \sum_i \sum_{\sigma} \alpha_i^\sigma$ $s.t. \:\: 0 \leq \alpha_i^\sigma \leq c \beta_i^\sigma \:,\:$ $\sum_{i=1}^m \sum_{\sigma} \alpha_i^\sigma \sigma = 0$ ## How the margin is affected

## Relation with the Classical Risk
Let's rewrite the classical risk R_{\phi}(X,Y,h) = R_{\phi}^{\beta}(X,h) - \frac{1}{m} \sum_i \beta_i^{-y_i} y_i h(x_i)
- R_{\phi}^{\beta}(X,h) is the $\beta$-risk - \frac{1}{m} \sum_i \beta_i^{-y_i} y_i h(x_i) is a penality term on the missclassified instances ## Iterative Algorithm
1. Learn $h$ $\:\:argmin_h \:\: N(h) + c R_{\phi}^{\beta}(X,h)$ 3. Estimate $y$ $\forall i=1..m,\:\:\:y_i = sign \left(\beta_i^{\text{+}1}-\frac{1}{2} \right)$ 2. Learn $\beta$ $\:\:argmin_{\beta} R_{\phi}^{\beta}(X,h)$
$s.t.\: \sum_{i=1}^{m}\beta_i^{\text{-}y_i} y_i h(x_i) = 0$
$\beta_i^{\text{-}1} + \beta_i^{\text{+}1} = 1$ ## Semi-Supervised Learning
with $m_l$ labeled instances and $m_u$ unlabeled instances
1. Initialization of $\beta$ - $\forall i=1..m_l \:\: \beta_i^{\sigma} = 1 \:\text{if}\: \sigma = y_i, 0 \:\text{otherwise} $ - $\forall i=m_l+1..m_u \:\: \beta_i^{\sigma} = 0.5$ 2. Iterative Algorithm - Learning $\beta$ of unlabeled set ## Results

WellSVM: Li Yu-Feng, Tsang Ivor W, Kwok James T, Zhou Zhi-Hua. Convex and scalable weakly labeled SVMs The Journal of Machine Learning Research, 2013. ## Perspectives: Differential Privacy How to accuratly learn while preserving the user privacy? Learn on bags of instances: - the labels of each single instance are unknown - we have access to the proportions of the classes per bag # Thanks for your attention

/ − automatically replaced by the author − automatically replaced by the title

← →